ステッピングモータ加速のためのパルス速度計算
この記事ではステッピングモータを加減速させる場合のパルス速度を計算してみます。こんな話題はきっと他に解説してる記事や書籍があろうかと思いますが、ぱっとは見つからず自分で計算してみたのでメモ程度に残しておきます。紹介する計算式は、マイコンの非力な計算能力でもタイマに設定する値を計算するのに十分計算可能な速さであることを検証済みです。
以前の記事 ステッピングモータを三角波で回してみた では固定の周期でモータを回していました。しかし、本当にやりたいのは停止状態から徐々に加速する、あるいは走行状態から減速して停止することです。そうしなければタイヤが滑ったりモータが脱調したりして正確な位置制御ができません。機体が転倒する恐れもあります。
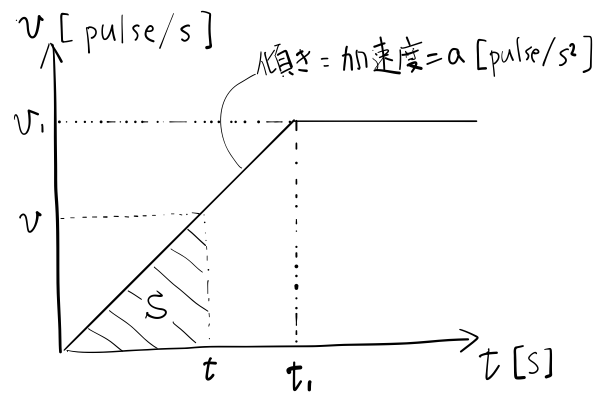
上図はパルス速度の時間変化を表したグラフです。ステッピングモータをこのグラフ通りの速度で回すことが最終的な目標となります。停止状態から等加速度で加速し、目標速度に達した後は一定の速度を維持します。
パルス速度の計算
加速度を $a\, \mathrm{[pulse/s^2]}$、$t\, \mathrm{[s]}$ の時点でのパルス速度を $v\, \mathrm{[pulse/s]}$ とします。$t_1$ 秒が経過した時点で目標速度 $v_1$ に到達するとして、モータ始動から $t$ 秒($0\leq t\leq t_1$)の間のパルス数 $S(t)$ は三角形の面積ですから $S(t) = vt/2$ となります。$v = at$ ですから $S(t) = at^2/2$ とも表せます。
今まで「パルス速度」と書いていましたが、求めたいのはパルス速度そのものではありません。マイコンのタイマに設定すべき時間です。パルスを出力してから次のパルスを出力するまでの待ち時間を求めたいのです。
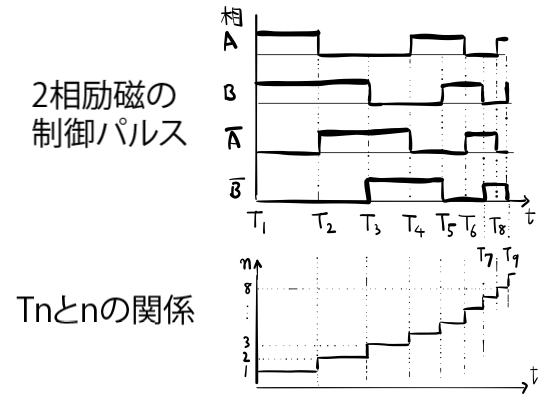
$n$ 個目のパルスを出力し始める時点での時刻を $T_n$ とします(上図)。時刻 0 で最初のパルスを出力し始めるとすると $T_1=0$ です。次のパルスを出力するまでに待つべき時間は $T_2-T_1$ で、次のパルスを出してからまた次のパルスを出力するまでに待つ時間は $T_3-T_2$ ですね。一般項は $T_{n+1}-T_n$ と表せます。以降、この値を求めていきます。
$T_n$ の定義より以下が成り立ちます。 $$ n = S(T_n) = \frac{aT_n^2}{2} = kT_n^2 $$ ただし $k=a/2$ と置きました。
$T_n$ を求めると $$ T_n = \sqrt{\frac{n}{k}} $$ となります。したがって差は $$ T_{n+1} - T_n = \sqrt{\frac{n+1}{k}} - \sqrt{\frac{n}{k}} $$ と計算できます。この計算値を元にしてタイマを設定し、タイマ割り込みによってパルスを出せば、加速度 $a$ で徐々に速くなるパルス列を生成することができます。
計算精度の向上
数式としては求まりましたが、これを愚直に計算すると値の精度が悪くなってしまいます。なぜなら、$n$ が大きくなるにつれて $T_{n+1}$ と $T_n$ は大きくなり、一方で差分 $T_{n+1}-T_n$ は大きくならない(むしろ小さくなる)からです。大きな値同士の引き算の結果が小さくなる場合、精度が落ちます1。
試しに 4 桁の精度で計算してみます。$1.100-1.000=0.100$ は差が 3 桁の精度で計算できますが、$100.1-100.0=0.1$ は同じ 0.1 であっても 1 桁まで精度が落ちてしまいます。引き算に使った 100.1 という数と 100.0 という数には本質的に小数点 2 桁目以降の情報が含まれていないので、その差である 0.1 にも小数点 2 桁目以降の情報が含まれないのは当然ですね。
どのくらいの精度が必要なのでしょうか。精度が落ちた後も許容できる精度を保つのであれば工夫は不要ですから、ちょっと検証してみます。前提として、ステッピングモータを三角波で回してみた と同様に制御することとします。モータを 1000 pulse/s で回そうと思うと周期は 1ms です。加速が完了した時点での総パルス数を $N$ とすると、$T_{N+1}-T_N=1\, \mathrm{[ms]}$ ということです。なめらかに加速することを考える場合、この周期が滑らかに増える必要があります。1000 pulse/s に対しての 1ms ですから、その 1/1000 である 1μs ずつ増えるようにすれば滑らかでしょうか。
次に $T_N$ の表現に必要な桁数を考えます。$a=100\, \mathrm{[pulse/s^2]}$ で 10 秒かけて加速するとしましょう。10 秒で目標速度に到達したとき $N=5000$ となります。$T_N=\sqrt{N/k}=10$ です。これを 1μs 単位で表現するには 24 ビット必要です($2^{23}<10\times 10^6<2^{24}$)。
float(単精度浮動小数点数)の仮数部は 23 ビットです。したがって float を使う限り愚直な計算方法では希望の精度を出せないことが分かりました。double なら十分ですが、後述するように STM32 で計算を高速化するには float が有利ですので、float のまま計算精度を上げる工夫を行います。先ほどの式を次のように変形します。
$$ T_{n+1} - T_n = \left(\sqrt{\frac{n+1}{k}} - \sqrt{\frac{n}{k}}\right)\frac{\sqrt{\frac{n+1}{k}} + \sqrt{\frac{n}{k}}}{\sqrt{\frac{n+1}{k}} + \sqrt{\frac{n}{k}}} = \frac{1}{\sqrt{k(n+1)} + \sqrt{kn}} $$
分母 $\sqrt{k(n+1)} + \sqrt{kn}$ は、$n$ が大きくなっても大きな数同士の加算になるため精度は落ちません。めでたし、めでたし。
根号計算の計算速度
$T_{n+1}-T_n$ の計算は三角波 PWM が 1 週するたびに実行する必要があります。そして、計算は三角波 PWM の 1 パルス以内に終わらせなくてはなりません。モータが最高速度 1000 pulse/s で回転しているとき、PWM の 1 パルスの周期は $1\, \mathrm{[ms]} / 16 = 62.5\, \mathrm{[\mu s]}$ となります。この計算以外にも必要な処理はありますので、62.5μs より十分短い時間で計算しなければなりません。
$T_{n+1}-T_n = 1/\left(\sqrt{k(n+1)} + \sqrt{kn}\right)$ には 2 回の根号(√)が登場します。このうち $\sqrt{k(n+1)}$ の方を保存しておき次の計算で再利用すれば、約 1/2 の処理時間までは高速化可能でしょう。ということで、根号計算 1 回の時間が分かればタイマ割り込み中に計算が完了するかどうかの目安となるはずです。
マイコンで根号の計算なんてとても遅いのでは?と思い、計算時間を計ってみました。計測プログラムは次の通りです。
double dt;
printf("sqrt\n");
dt = 0;
start = DWT->CYCCNT;
for (int i = 0; i < 100000; i++) {
dt += sqrt(i);
}
elapsed = DWT->CYCCNT - start;
printf("dt=%f elapsed=%9lu avg=%2lu.%05lu[us]\n",
dt, elapsed, elapsed / 80 / 100000, (elapsed / 80) % 100000);
2 重根の計算結果を変数に足し込む操作を 100000 回繰り返し、最後にかかった総クロック数と 1 ループあたりの平均時間を表示します。DWT->CYCCNT を読むと CPU クロックカウンタの値が読めます2。CPU クロックは 80MHz です。
計測結果は次の通りです。使用したマイコンは STM32L476RG です。
| 関数名 | 100000 ループにかかったクロック数 | 1 ループあたり平均時間(μs) |
|---|---|---|
| sqrt | 150430640 | 18.80383 |
| julery_isqrt | 16597237 | 2.07465 |
| mcrowne_isqrt | 9784486 | 1.22306 |
| arm_sqrt_f32 | 6002935 | 0.75036 |
| sqrtf | 5302482 | 0.66281 |
julery_isqrt と mcrowne_isqrt は整数バージョンの 2 重根関数です。Paul Hsieh's Square Root page で紹介されている関数をそのまま使いました。これら 2 つの関数については、 double dt; の代わりに uint32_t t; と定義した変数を使って和を計算するようにしました。dt を使ってしまうと double と整数の間の型変換が毎ループ発生してしまい、それが計測に影響するからです。同様の理由で arm_sqrt_f32 と sqrtf では float ft; と定義した変数を使いました。
筆者は驚きました。sqrt が遅いのはまあそうかなと思いますが3、整数バージョンの、しかもそれなりに高速化されているであろう計算プログラムより、float で計算する方がずっと速いのです!これは、使っているマイコン STM32L476RG が FPU 演算器を持っているおかげだと思います。ちなみに arm_sqrt_f32 は CMSIS に含まれる関数でして、内部で sqrt を呼び出しています。
この記事を書き始めたときは、sqrt は遅いから整数バージョンの関数を使いましょうというストーリーにするつもりでした。sqrt でも 19μs 程度ですから、まあなんとか使えそうな気はしますが、でもやっぱり 62.5 μ秒のうち 19μs はちょっと時間をかけすぎなので、高速な整数バージョンを使いましょう、という流れです。しかし sqrtf であれば超高速に計算できることが分かりました。sqrtf は math.h をインクルードするだけで使えますから、これを使うに超したことはありませんね。
- [1]: 情報落ち
- [2]: Silicon Labs EFM32:コードの実行時間を測定する方法はありませんか? - 半導体事業 - マクニカ を参考にしました。
- [3]:
doubleを使うのでソフトウェア的な計算になってしまうのでしょう。
この記事を参照しているブログ内記事はありません。